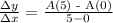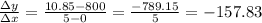In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
A(t) = 800e^(-0.86t)
Step 02:
Rate of change
t1 = 0
A(t) = 800e^(-0.86t)
A(t) = 800e^(-0.86*0)
A(0) = 800
t2 = 5
A(t) = 800e^(-0.86t)
A(t) = 800e^(-0.86*5)
A (t) = 800e^(-4.3)
A(5) = 10.85
Step 03: