Answer:
Explanations:
According to the question, we need to determine which of the signs will fit in that will make the expression a binomial.
In simple terms, a binomial is a two-term algebraic expression that contains variable, coefficient, exponents, and constant.
We need to determine the required sign by using the trial and error method.
Using the positive sign (+) first, we will have:
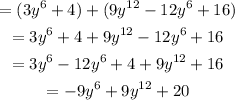
Using the product sign, this will be expressed as:
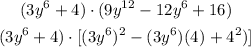
According to the sum of two cubes;
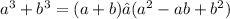
Comparing this with the expression above, we will see that a = 3y^6 and
b = 4. This means that the resulting expression above can be written as a sum of two cubes to have;
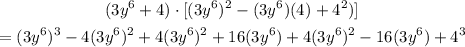
Collect the like terms:
![undefined]()