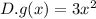Given:
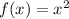
Let's find g(x).
From the given graph, we can see the graph of g(x) is compressed horizontally from f(x).
Thus, to find g(x) aply the transformation rules for function.
We have:
Horizontal compression of b units ==> f(bx)
Given the point on g(x):
(x, y) ==> (2, 12)
Let's solve for the value of the compressed factor.
We have:
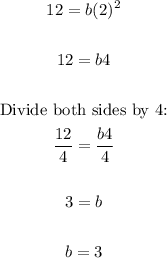
This means the graph of f(x) was compressed horizontally by a factor of 3 to get g(x).
Thus, to write the function for g(x), we have:
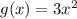
ANSWER: