Question

Refer to the diagram below to prove that the exterior angle equals the

Answer 1

To prove that the sum of the remote interior angles and the exterior angle have the same value, we recall 2 things:

1.- the inner angles of a triangle add up 180 degrees

2.- angle 3 and angle 4 are supplementary which means that they add up 180 degrees.

`\begin{gathered} \measuredangle1+\measuredangle2+\measuredangle3=180^(\circ) \\ \measuredangle3+\measuredangle4=180^(\circ) \\ \Rightarrow \\ \measuredangle1+\measuredangle2+\measuredangle3=\measuredangle3+\measuredangle4 \\ \Rightarrow \\ \measuredangle1+\measuredangle2=\measuredangle4 \end{gathered}`

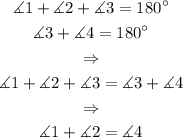
Answer:

They are linear pair and therefore supplementary.

Triangle sum theorem.

Substitution.

Subtraction property of equality.