GIven:
The equation of a line is 15x+12y=-108.
The objective is to find the slope of the perpencidular line.
It is known that the equation of straight line is,

Here, m represents the slope of the equation and c represents the y intercept of the equation.
Let's find the slope of the given equation by rearranging the eqation.
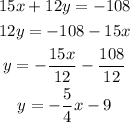
By comparing the obtained equation with equation of striaght line, the value of slope is,
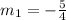
THe relationship between slopes of a perpendicular lines is,
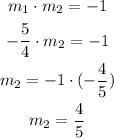
Hence, the value of slope of perpendicular line to the given line is 4/5.