Question

Five pulse rates are randomly selected from a set of measurements. The five pulso rates have a mean of 74 4 boats per minute. Four of the pulse rates are 84, 66, 79, and 57a. Find the missing valueb. Suppose that you need to create a list of n values that have a specific known mean. Some of thon values can be freely selected. How many of the n values can be froely assigned before the remaining valuesare determined? (The result is referred to as the number of degrees of freedom.)a. The missing value isbeats per minute

Answer 1

(a)

We have five pulse rates randomly selected with a mean of 74.4 beats per minute. We have four pulse rates given. We let x be the value of the fifth pulse rate. We have n equals 5 here since we have sample space of 5. We illustrate the mean of the pulse rates as

Let's solve for the value of x. We have

`\begin{gathered} 74.4=(286+x)/(5) \\ 286+x=(74.4)\cdot5 \\ 286+x=372 \\ x=372-286 \\ x=86 \end{gathered}`

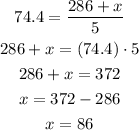
Hence, the missing value is equal to 86.

Answer: 86

(b) The number of degrees of freedom is calculated using the equation

`\text{Degrees of freedom}=n-1`

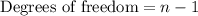
We already identified that the sample space n is equal to 5. Hence, the degrees of freedom is equal to

`\text{Degrees of freedom}=5-1=4`

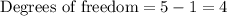
Answer: 4