Answer:
The three correct corresponding pairs that gives the same area are;
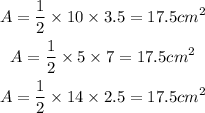
The areas are the same in each case because the product of each pair is the same.
Step-by-step explanation:
Given the base and height pairs in the question.
Let us use the corresponding pairs that gives the same area.
Firstly, for the first pair;
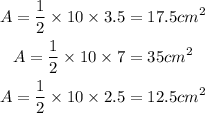
Secondly, the second pair is;
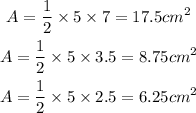
Thirdly, the third pair;

Therefore, the three correct corresponding pairs that gives the same area are;
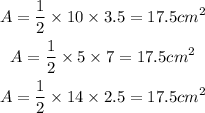
The areas are the same in each case because the product of each pair is the same.