The symmetry of a quadratic equation is given by the line that passes through its vertex, so in order to find the axis of symmetry we need to find the coordinate of the vertex, which is done below.

Where "a" is the number multiplying the square factor and "b" is the number multiplying the factor that isn't squared. To find these two constants we need to expand the equation given.
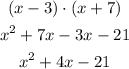
We have that a = 1 and b = 4, therefore:
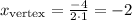
The axis of symmetry for this quadratic equation is x=-2.