When two lines are perpendicular to each other, their slopes would be a negative inverse of each other. This simply means the slope of a line perpendicular to the one in the question should be equal to the negative inverse of the one we have here. Let us begin by calculating the slope of this line.
When you are given two endpoints, the slope is derived as;

When the coordinates are (0, 3) and (-1.5, 0)
That is, when x = 0 then y = 3 (observe the point where the line touches the vertical axis), and when x = -1.5, then y = 0 (observe the point where the line touches the horizontal axis)
Therefore, the coordinates (0, 3) and (-1.5, 0) are now your (x1, y1) and (x2, y2)
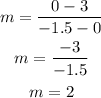
Therefore the slope of a line perpendicular to the one on the graph is -1/2.