Solution
- Let the length of the rectangle be x
- Let the width of the rectangle be y.
- Thus, we can interpret the lines of the question as follows:
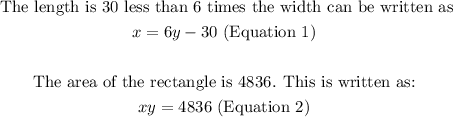
- Now, let us solve these two equations simultaneously.
- We shall proceed by solving the system of equations graphically.
- Wherever the graphs of Equation 1 and Equation 2 intersect represents the solution to the system of equations
- The plot of the equations is given below
- Observe that the graphs cross at two points. The first point is positive and the other, negative.
- Since we cannot have negative lengths (x) or width (y), we can discard the negative coordinates.
- Thus, the length (x) and width (y) are given below:
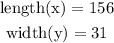
Final Answer
The length of the rectangle is 156 feet