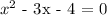Question

Write the equation of a quadratic in general form, given its solutions.x=4 ; x=-1

Answer 1

The given solutions of the quadratic equation:

x = 4 and x = -1

First we make them factors of the equation:

x= 4 becomes:

`x-4\text{ = 0}`

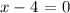
and x = -1 becomes:

`x\text{ + 1 = 0}`

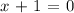
So (x-4) and (x+1) are the factors.

To get the general quadratic equation, we would expand the factors

`\begin{gathered} (x-4)(x+1)\text{ = 0 } \\ x(x+1)\text{ -4(x+1) = 0} \\ x^2+x\text{ -4x-4 = 0} \end{gathered}`
`\begin{gathered} Adding\text{ like terms} \\ x^2-3x-4\text{ = 0} \end{gathered}`

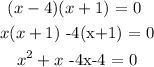
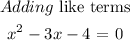
The general quadratic equation:

`x^2\text{ - 3x - 4 = 0}`