Answer:
To convert the polar equation to a rectangular equation .
Given polar equation is,
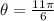
we know the convertion of polar coordinates (r,theta) to rectangular equation as,
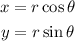
we get,
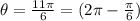
Substitute this in the above equation we get,
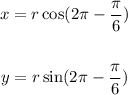
Solving we get,
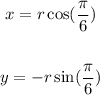
we get,
![x=r(\frac{\sqrt[]{3}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/ww6063ijwadsipv15sgl1g8pa0nu9ekhvf.png)
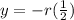
Substitute r=-2y in x we get,
![x=-2y(\frac{\sqrt[]{3}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/xu6167xxvgdici4q52k7rq4njqd29o7e0b.png)
![y=-\frac{x}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/38o8f2kzm26blveohd8ewqbd4z8vxf03ss.png)
![y=-\frac{\sqrt[]{3}x}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/n7mjkl7vqxdqtee5snx13yi3sftnqyw58d.png)
The required rectangular form of the given plar equation is,
![y=-\frac{\sqrt[]{3}x}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/n7mjkl7vqxdqtee5snx13yi3sftnqyw58d.png)