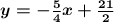Question

Im not sure the steps to this math problem, from step one to step three

Answer 1

Step 1

The equation of the second line is written in standard form. To know the slope of this line, we can rewrite its equation in slope-intercept form by solving for y.

`\begin{gathered} ax+by=c\Rightarrow\text{ Standard form} \\ y=mx+b\Rightarrow\text{ Slope-intercept form} \\ \text{ Where m is the slope and b is the y-intercept} \end{gathered}`

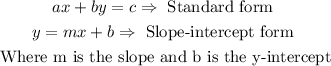
Then, we have:

`\begin{gathered} 4x-5y=-10 \\ \text{ Subtract 4x from both sides of the equation} \\ 4x-5y-4x=-10-4x \\ -5y=-10-4x \\ \text{Divide by -5 from both sides of the equation} \\ (-5y)/(-5)=(-10-4x)/(-5) \\ y=(-10)/(-5)-(4x)/(-5) \\ y=2+(4)/(5)x \\ \text{ Reorganize} \\ y=(4)/(5)x+2 \\ \text{ Then} \\ $$\boldsymbol{m=(4)/(5)}$$ \end{gathered}`

Now, two lines are perpendicular if their slopes satisfy the following equation:

`\begin{gathered} m_1=-(1)/(m_2) \\ \text{ Where }m_1\text{ is the slope of the first equation and} \\ m_2\text{ is the slope of the second equation} \end{gathered}`

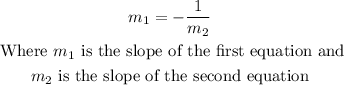
In this case, we have:

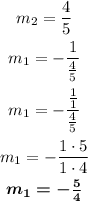
`\begin{gathered} m_2=(4)/(5) \\ m_1=-\frac{1}{(4)/(5)_{}} \\ m_1=-\frac{(1)/(1)}{(4)/(5)_{}} \\ m_1=-(1\cdot5)/(1\cdot4) \\ $$\boldsymbol{m}_{\boldsymbol{1}}\boldsymbol{=-(5)/(4)}$$ \end{gathered}`Step 2

Since we already have a point on the line and its slope, then we can use the point-slope formula:

`\begin{gathered} y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope formula} \\ \text{ Where } \\ m\text{ is the slope and} \\ (x_1,y_1)\text{ is a point through which the line passes} \end{gathered}`

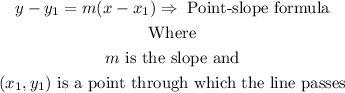
Then, we have:

`\begin{gathered} (x_1,y_1)=(6,3) \\ m=-(5)/(4) \\ y-3=-(5)/(4)(x-6) \\ \text{ Apply the distributive property} \\ y-3=-(5)/(4)\cdot x-(5)/(4)\cdot-6 \\ y-3=-(5)/(4)x+(5)/(4)\cdot6 \\ y-3=-(5)/(4)x+(30)/(4) \\ \text{ Add 3 from both sides of the equation} \\ y-3+3=-(5)/(4)x+(30)/(4)+3 \\ y=-(5)/(4)x+(30)/(4)+(12)/(4) \\ y=-(5)/(4)x+(30+12)/(4) \\ y=-(5)/(4)x+(42)/(4) \\ \text{ Simplify} \\ y=-(5)/(4)x+(21\cdot2)/(2\cdot2) \\ y=-(5)/(4)x+(21)/(2) \end{gathered}`Step 3

Therefore, the equation of the line that passes through the point (6,3) that is perpendicular to the line 4x - 5y = -10 is

`$$\boldsymbol{y=-(5)/(4)x+(21)/(2)}$$`