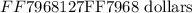Question

If you borrow $100 for 3 years at anannual interest rate of 9%, howmuch will you pay altogether?

Answer 1

We are to determine the amount that you have pay back after borrowing a principal amount ( P ) for ( t ) number of years which is compounded annualy at rate ( R ).

You borrowed a principal amount of:

`P\text{ = \$100}`

The time duration for which we have borrowed the money for is:

`t\text{ = 3 years}`

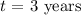
The annual interest rate coumpounded each year is:

`R\text{ = 9\% / year}`

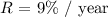
Step 1: Determine the simple interest that accumulated at the end of ( t ) years.

The folllowing formula is used to determine the simple interest that the borrower has to pay once the period of borrowing/lending is over i.e ( t ) years.

The simple interest is the proportional rate of interest ( R ) and the initial borrowed/loaned amount called principal amount ( P ).

`\text{Simple Interest ( I ) = }(P\cdot R\cdot t)/(100)`

Use the above simple interest formula ( I ) by plugging in the respective values as follows:

`\text{Simple Interest ( I ) = }(100\cdot9\cdot3)/(100)\text{ = \$27}`

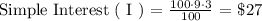
Therefore, the total amount of interest that the borrower must pay as an extra ( over the borrowed amount ) is $27.

Step 2: Determine the total amount that is to be returned/paid to the lender

The total amoun that is to be paid by the borrower ( you ) to the lender is the principal amount borrowed ( P ) and the amount of interest accumulated for the contractual time period i.e ( I ).

`\begin{gathered} \text{Total amount to be paid = P + I} \\ \text{Total amount to be paid = \$100 + \$27} \\ \text{Total amount to be paid = }127 \end{gathered}`

Therefore, the amount that you need to pay altogether is:

`\textcolor{#FF7968}{127}\text{\textcolor{#FF7968}{ dollars}}`