Question

If p(x) is a polynomial function where p(x) = 3(x + 1)(x - 2)(2x-5)a. What are the x-intercepts of the graph of p(x)?b. What is the end behavior (as x→ ∞, f(x)→?? and as x→ -∞, f (x)→ ??) of p(x))?c. Find an equation for a polynomial q(x) that has x-intercepts at -2, 3⁄4, and 7.

Answer 1

Hello there. To solve this question, we have to remember some properties about polynomial functions.

Given the polynomial function

`p(x)=3(x+1)(x-2)(2x-5)`

We want to determine:

a) What are the x-intercepts of the graph of p(x)?

For this, we have to determine the roots of the polynomial function p(x). In this case, we have to determine for which values of x we have

`p(x)=0`

Since p(x) is written in canonical form, we find that

`p(x)=3(x+1)(x-2)(2x-5)=0`

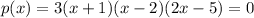
A product is equal to zero if at least one of its factors is equal to zero, hence

`x+1=0\text{ or }x-2=0\text{ or }2x-5=0`

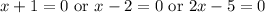
Solving the equations, we find that

`x=-1\text{ or }x=2\text{ or }x=(5)/(2)`

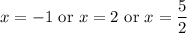
Are the solutions of the polynomial equation and therefore the x-intercepts of p(x).

b) What is the end-behavior of p(x) as x goes to +∞ or x goes to -∞?

For this, we have to take the limit of the function.

In general, for polynomial functions, those limits are either equal to ∞ or -∞, depending on the degree of the polynomial and the leading coefficient.

For example, a second degree polynomial function with positive leading coefficient is a parabola concave up and both limits for the function as x goes to ∞ or x goes to -∞ is equal to ∞.

On the other hand, an odd degree function usually has an odd number of factors (the number of x-intercepts in the complex plane) hence the limits might be different.

In this case, we have a third degree polynomial equation and we find that, as the leading coefficient is positive and all the other factors are monoic, that

`\begin{gathered} \lim_(x\to\infty)p(x)=\infty \\ \\ \lim_(x\to-\infty)p(x)=-\infty \end{gathered}`

That is, it gets larger and larger when x is increasing arbitrarily, while it get smaller and smaller as x is decreasing.

c) To find the equation for a polynomial q(x) that has x-intercepts at -2, 3/4 and 7.

The canonical form of a polynomial of degree n with x-intercepts at x1, x2, ..., xn and leading coefficient equals a is written as

`f(x)=a\cdot(x-x_1)(x-x_2)\cdots(x-x_n)`

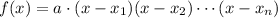
So in this case, there are infinitely many polynomials satisfying this condition. Choosing a = 1, we find that q(x) is equal to

`\begin{gathered} q(x)=(x-(-2))\cdot\left(x-(3)/(4)\right)\cdot(x-7) \\ \\ \boxed{q(x)=(x+2)\cdot\left(x-(3)/(4)\right)\cdot(x-7)} \end{gathered}`

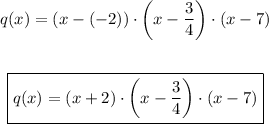
These are the answers to this question.