Question

A grocer mixed grape juice which costs $1.50 per gallon with cranberry juice whichcosts $2.00 per gallon. How many gallons of each should be used to make 200 gallons of cranberry/grape juice which will cost $1.75 per gallon?

Answer 1

Let x be the amount of gallons of grape juice we are using to get the mixture we want. Let y be the amount of gallons of cranberry juice used to get the desired mixture.

Since we are told that we want a total of 200 gallons of the new mixture, this amount would be the sum of gallons of each liquid. So we have this equation

`x+y=200`

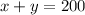
To find the values of x and y, we need another equation relating this variables. Note that since we have 200 gallons of the new mixture and the cost per gallon of the new mixture is 1.75, the total cost of the new mixture would be

`1.75\cdot200=350`

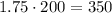
As with quantities, the total cost of the new mixture would be the cost of each liquid. In the case of the grape juice, since we have x gallons and a cost of 1.50 per gallon, the total cost of x gallons of grape juice is

`1.50\cdot x`

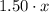
In the same manner, the total cost of the cranberry juice would be

`2\cdot y`

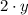
So, the sum of this two quantites should be the total cost of the new mixture. Then, we get the following equation

`1.50x+2y=350`

If we multiply this second equation by 2 on both sides, we get

`3x+4y=700`

Using the first equation, we get

`x=200\text{ -y}`

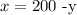
Replacing this value in the second equation, we get

`3\cdot(200\text{ -y)+4y=700}`

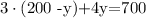
Distributing on the left side we get

`600\text{ -3y+4y=700}`

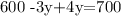
operating on the left side, we get

`600+y=700`

Subtracting 600 on both sides, we get

`y=700\text{ -600=100}`

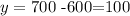
Now, if we replace this value of y in the equation for x, we get

`x=200\text{ -100=100}`

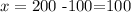
Thus we need 100 gallons of each juice to produce the desired mixture.