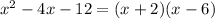Question

Factor the Expression. If the expression cannot be factored, say so. 8.) x^2 - 4x - 12

Answer 1

To factor an expression of the form:

`x^2+bx+c`

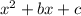
we find two numbers B and C that fulfills the following properties:

`\begin{gathered} B+C=b \\ BC=c \end{gathered}`

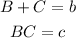
In this case we have b=-4 and c=-12. We can choose B=-6 and C=2. Then we write the expression as:

`x^2-4x-12=x^2-6x+2x-12`

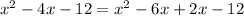
and we factor the common factors in the first two and last terms:

`\begin{gathered} x^2-4x-12=x^2-6x+2x-12 \\ =x(x-6)+2(x-6) \\ =(x+2)(x-6) \end{gathered}`

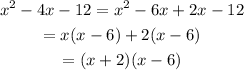
Therefore:

`x^2-4x-12=(x+2)(x-6)`