Answer:
The system of equations is:
• C(x)=2400+60x
,
• R(x)=120x
The number of bicycles to break even = 40
Explanation:
Let the number of bikes sold = x
• The operating cost of the store per month = $2400
,
• Cost Price Per bike = $60
Thus, the total monthly cost for the store:
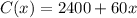
Next, the average selling price of each bicycle is $120, therefore, the monthly revenue of the store:
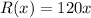
The store breaks even when the cost equals its revenue.
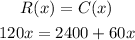
We then solve for x:
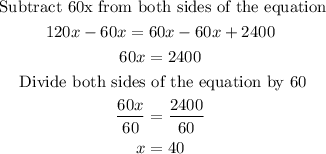
The store must sell 40 bicycles in order to break even.