In order to calculate the surface area of the cone, first let's calculate its slant height.
If the diameter is 5 cm, the radius is 2.5 cm. Now, using the Pythagorean theorem, we can calculate the slant height s:
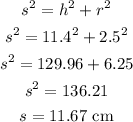
Now, we can calculate the surface area using the formula below:
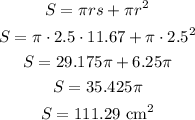
Rounding to the nearest square centimeter, we have a surface area of 111 cm².