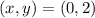We are given the following system of equations:
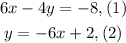
To solve this system by substitution we will replace the value of "y" from equation (2) in equation (1)
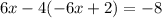
Now we use the distributive property:

Now we add like terms:
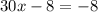
Now we add 8 to both sides:
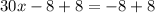
Solving the operations:

Dividing by 30:
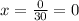
Therefore x = 0. Now we replace the value of "x" in equation (2):
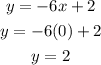
Therefore, the solution of the system is: