In general, a dilation is the outcome of applying the following transformation on a point,
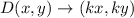
Where k is the scale factor, this kind of dilation is about the origin, and we will use it since the problem does not specify otherwise.
In our case, the transformation is
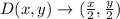
Then,
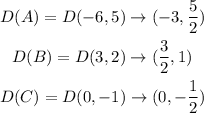
On the other hand, a reflection over the x-axis is given by the following transformation.
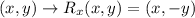
Then, in our case,
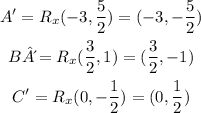
Thus, the answers are
A'=(-3,-5/2)
B'=(3/2,-1)
C'=(0,1/2)