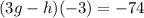Question

I need help to find the indicated operation:g(x)= -x^2 +4xh(x)= -4x-1Find (3g-h)(-3)

Answer 1

We have the following functions:

`\begin{gathered} g\mleft(x\mright)=-x^2+4x \\ h\mleft(x\mright)=-4x-1 \end{gathered}`

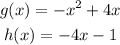
And we need to find:

`(3g-h)(-3)`

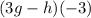
Step 1. Find 3g by multiplying g(x) by 3:

`\begin{gathered} g(x)=-x^2+4x \\ 3g=3(-x^2+4x) \end{gathered}`

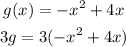
Use the distributive property to multiply 3 by the two terms inside the parentheses:

`3g=-3x^2+12x`

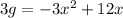
Step 2. Once we have 3g, we subtract h(x) to it:

`3g-h=-3x^2+12x-(-4x-1)`

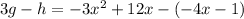
Here we have 3g and to that, we are subtracting h which in parentheses.

Simplifying the expression by again using the distributive property and multiply the - sign by the two terms inside the parentheses:

`3g-h=-3x^2+12x+4x+1`

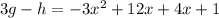
Step 4. Combine like terms:

`3g-h=-3x^2+16x+1`

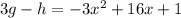
What we just found is (3g-h)(x):

`(3g-h)(x)=-3x^2+16x+1`

Step 5. To find what we are asked for

`\mleft(3g-h\mright)\mleft(-3\mright)​`

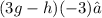
We need to evaluate the result from step 4, when x is equal to -3:

`(3g-h)(-3)=-3(-3)^2+16(-3)+1`

Solving the operations:

`(3g-h)(-3)=-3(9)^{}-48+1`
`(3g-h)(-3)=-27^{}-48+1`
`(3g-h)(-3)=-74`

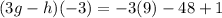
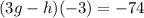
Answer:

`(3g-h)(-3)=-74`