Question

Since January 1, 1960, the population of Slim Chance has been described by the formula P = 27000(0.95)^t, where P is the population of the city t years after the start of 1960. At what rate was the population changingon January 1, 19702?numerical rate of change= ___ people per year

Answer 1

We have to calculate the rate of change of the population P(t) at January 1, 1970 (t = 10).

The expression for P(t) is:

`P(t)=27000\cdot0.95^t`

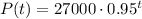
The rate of change will be given by the first derivative of P(t):

`(dP)/(dt)=27000\cdot\ln (0.95)\cdot0.95^t`

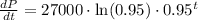
Then, we can calculate the value of the rate of change when t = 10, by replacing t with 10 in the last expression. We then will get:

`\begin{gathered} (dP)/(dt)(100)=27000\cdot\ln (0.95)\cdot0.95^(10) \\ (dP)/(dt)(100)\approx27000\cdot(-0.0513)\cdot0.5987 \\ (dP)/(dt)(100)\approx-829 \end{gathered}`

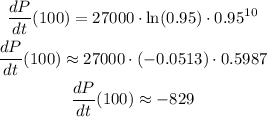
The population, on January 1st 1970, is decreasing at a rate of 829 people per year.

Answer: numerical rate of change= -829 people per year