Question

6. Create a systems of inequalities to represent the graph below

Answer 1

System of inequalities

We are given the graph where two lines represent the solution of a system of inequalities.

The solution is the double-shaded region of the graph.

We need to find the equation of the blue line and the red line and then convert them to inequalities.

Let's start with the blue line. We need to find two clear points through which it passes. These are (0,6) and (2,0). Now we write the equation of the line when knowing two points (the point-point form):

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`
`\begin{gathered} \displaystyle y-6=(0-6)/(2-0)(x-0)=-3x \\ \text{Adding 6:} \\ y=-3x+6 \end{gathered}`

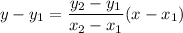
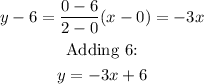
For the red line, the points are (0,0) and (2,2):

`\begin{gathered} y-0=(2-0)/(2-0)(x-0)=x \\ y=x \end{gathered}`

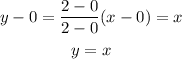
Now we have the equations of the lines, we must convert the equation to inequality by inserting one of these symbols instead of the equal sign:

> ≥ < ≤

For the blue line, the equation of the line is:

y = -3x + 6

Testing the origin (0,0):

0 = 0 + 6

0 = 6

To convert this to a true inequality we must replace the = for < or ≤

Since the blue line is solid, the points on the line belong to the solution, thus the first inequality is:

y ≤ -3x + 6

Now for the red line. The equation is

y = x. Let's test the point (2,1)

1 = 2

We must use the sign ≤ to make the expression true, thus the second inequality is:

y ≤ x

Thus, the system of inequalities is:

y ≤ -3x + 6

y ≤ x