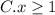Question

Which choice is equivalent to the quotient shown here for acceptablevalues of x?25(x - 1) = 5(x - 1)?A.5(x - 1)B. 125(x - 1)C. V25(x - 1) -5(x - 1)?D. V5(x - 1)SUBMIT

Answer 1

Given the expression:

`\sqrt[]{28(x-1)}/\sqrt[]{8x^2}`

`\frac{\sqrt[]{28(x-1)}}{\sqrt[]{8x^2}}`

Let's determine the inequality that represents all the values of x.

Here, we are to find the domain.

Let's solve for x.

Set the radicand in the numerator and denominator to be greater or equal to zero.

We have:

`(28(x-1)\ge0)/(8x^2\ge0)`

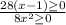
For the numerator, we have:

`\begin{gathered} 28(x-1)\ge0 \\ \text{Divide both sides by 28:} \\ (28(x-1))/(28)\ge(0)/(28) \\ \\ x-1\ge0 \\ \text{Add 1 to both sides:} \\ x-1+1\ge0+1 \\ x\ge1 \end{gathered}`

For the denominator, we have:

`\begin{gathered} 8x\ge0 \\ x\ge(0)/(8) \\ x\ge0 \end{gathered}`

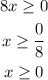
Therefore, the possible x-values for which the quotient is defined is all positive integers greater or equal to 1.

Thus, we have:

`x\ge1`

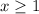
ANSWER:

`C.x\ge1`