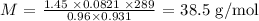Answer:
Step-by-step explanation:
Here, we want to get the molar mass of the gas
Let us call it M
From the ideal gas equation, we can get the number of moles of the gas
Mathematically:
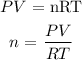
Also, n is the mass divided by the molar mass of the gas:
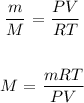
Where:
M is the molar mass that we want to calculate
m is the mass of the gas sample which is 1.45 g
P is the gas pressure which is 733 torr (to convert to atm, we multiply by 0.00131579 : 733 * 0.00131579 = 0.96 atm)
V is the volume which is 931 mL (We convert to L by dividing by 1000:
931/1000 = 0.931 L)
R is the molar gas constant which is 0.0821 L.atm/mol.K
T is the temperature that we convert to K by adding 273 K : 273 + 16 = 289 K)
Substituting the values, we have it that: