Step-by-step explanation:
Consider the following function:
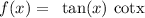
First, let's find the derivative of this function. For this, we will apply the product rule for derivatives:
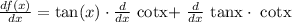
this is equivalent to:

or
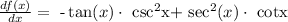
now, this is equivalent to:
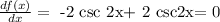
thus,
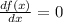
Now, to find the slope of the function f(x) at the point (x,y) = (1,1), lug the x-coordinate of the given point into the derivative (this is the slope of the function at the point):
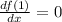
Notice that this slope matches the slope found on the graph of the function f(x), because horizontal lines have a slope 0:
We can conclude that the correct answer is:
Answer:
The slope of the graph f(x) at the point (1,1) is
