Question

Do you know how to solve? I got 3.99 for the mean (it was correct)For the sample standard deviation I got 1.1285 ( but it was wrong)

Answer 1

Step-by-step explanation

Given the sample below, we are asked to find the mean and the standard deviation.

Part A

We can find the mean below using the formula

`\begin{gathered} \text{Mean}=\frac{\sum ^{}_{}x}{n} \\ \text{where x is the sample value and n is the sample size} \end{gathered}`

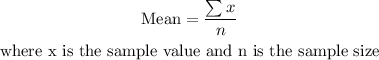
Therefore,

`\text{Mean }=(79.8)/(20)=3.99`

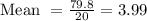
Answer =3.99

Part B

The standard deviation of the sample size can be found using the formula below;

`\begin{gathered} S.D=\sqrt[]{\sum ^{}_{}\frac{(x-\bar{x})^2}{N-1}} \\ =\sqrt[]{(20.938)/(19)} \\ =\sqrt[]{1.102} \\ =1.05 \\ \end{gathered}`

Answer: 1.05