Question

A bunny and a tortoise start a race from rest. The bunny accelerates at a rate "a" for a time "t" until it reaches itsmaximum speed (vb) after traveling a distance d_b. The tortoise accelerates at a rate one fourth as great as the bunny andtakes three times as long to reach its maximum speed of vt after traveling a distance d_t.a) What is the maximum speed of the tortoise? Answer in terms of vbb)How far did the tortoise travel? Answer in terms of db

Answer 1

We are given that a Bunny starts a race from rest, this means that its initial speed is zero:

`v_(b0)=0,(1)`

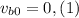
We are also given that it accelerates at a rate "a" for a time "t" and reaches its maximum speed. We can use the following equation of motion to relate the final speed with its acceleration:

`v_b=at,(2)`

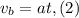
We are also given that it travels a distance "d". We can use the following equation of motion to relate the distance travel with the velocity and the acceleration:

`2ad_b=v^2_b,(3)`

Now. We turn our attention to the turtle. We are told that its acceleration is one-fourth of the acceleration of the bunny, therefore, we have:

`a_t=(1)/(4)a`

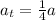
And it also says that it takes 3 times as long to reach its maximum speed, therefore the time of the turtle is:

`t_t=3t`

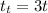
Now we use the equation of motion that relates velocity with time and acceleration for turtle:

`v_t=a_tt_t`

Since we are required to express this velocity in terms of the final velocity of the bunny we replace the values of acceleration and time of the turtle that we determined previously:

`v_t=((1)/(4)a)(3t)`

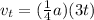
Rearranging terms:

`v_t=(3)/(4)at`

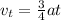
From the equation of motion from the bunny we know that the product of acceleration and time of the bunny equals its final velocity , therefore:

`v_t=(3)/(4)v_b`

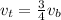
And thus we have determined the final velocity of the turtle in terms of the final velocity of the bunny.

Now we are told to determine the final velocity in terms of the distance traveled by the bunny. First, we will use the equation of motion that relates the distance, the acceleration, and the time with the final velocity:

`2a_td_t=v^2_t`

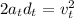
Now we replace the value of the acceleration:

`2((1)/(4)a)d_t=v^2_t`

Simplifying:

`(1)/(2)ad_t=v^2_t`

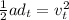
Now we use the relationship between velocities we determined in part A:

`(1)/(2)ad_t=((3)/(4)v_b)^2`

Simplifying:

`(1)/(2)ad_t=(9)/(16)v^2_b`

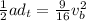
From equation (3) we can replace the value of the velocity of the bunny:

`(1)/(2)ad_t=(9)/(16)*2ad_b`

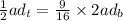
We can cancel out the acceleration:

`(1)/(2)d_t=(9)/(16)*2d_b`

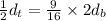
Now we multiply both sides by 2:

`d_t=2*(9)/(16)*2d_b`

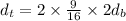
Simplifying:

`d_t=(9)/(4)d_b`

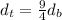
And thus we have found the distance traveled by the turtle in terms of the distance traveld by the bunny.