1 Answer

Ask a Question

Doolan · Answer 1 · 2023-10-07T09:23:44+0000

Step-by-step explanation

Step 1

diagram

so

Step 2

let

a)total area= side1*side 2

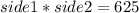
and

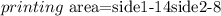
$printing\text{ area=\lparen side1-14\rparen\lparen side2-8\rparen}$

Step 3

solve

let

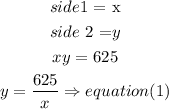
$\begin{gathered} side1\text{ = x} \\ side\text{ 2 =}y \\ xy=625 \\ y=(625)/(x)\Rightarrow equation(1) \end{gathered}$

and in teh second equation we have

$\begin{gathered} pr\imaginaryI nt\imaginaryI ng\text{area=}\operatorname{\lparen}\text{s}\imaginaryI\text{de*1-14}\operatorname{\rparen}\operatorname{\lparen}\text{s}\imaginaryI\text{de*2-8}\operatorname{\rparen} \\ A=(x-14)(y-8) \\ replace\text{ the y value} \\ A=(x-14)((625)/(x)-8) \\ A=(625x)/(x)-(8750)/(x)-8x+112) \\ A=-(8750)/(x)+625-8x+112 \\ dA=(8750)/(x^2)-8 \\ (8750)/(x^2)=8 \\ x^2=(8750)/(8) \\ x=\sqrt[\placeholder{⬚}]{(8750)/(8)} \\ x=33 \end{gathered}$

replace to find y

$\begin{gathered} y=(625)/(x)\operatorname{\Rightarrow}equat\imaginaryI on(1) \\ y=(625)/(33) \\ y=18.9 \end{gathered}$

so

the maximum area is

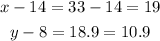
$\begin{gathered} x-14=33-14=19 \\ y-8=18.9=10.9 \end{gathered}$

so, the greates area is

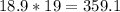
therefore, the answer is

359.1 square cm

I hope this helps you

You are designing a poster with an area of 625 cm2 to contain a printing area in the-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions