The geometric progression has the form:
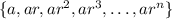
We have the information about the second term, a*r:
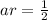
We know that the common ratio is
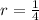
So from this information we can get the coefficient a:
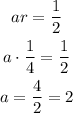
And we also know that the last term is 1/128, that is
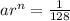
From this one we can find n:
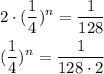
We can apply the property of the logarithm of power to get n:
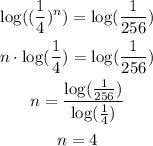
Be careful, because n is not the number of terms. The number of terms is n+1, so the G.P. has 5 terms