Question

Can you please help with 44For the following exercise, sketch a graph of the hyperbola, labeling vertices and foci

Answer 1

We have the following equation of a hyperbola:

`4x^2+16x-4y^2+16y+16=0`

Let's divide all the equations by 4, just to simplify it

`x^2+4x-y^2+4y+4=0`

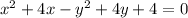
Just to make it easier, let's put the term if "x" isolated

`x^2+4x=y^2-4y-4`

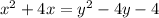
Now we can complete squares on both sides, just remember that

`\begin{gathered} (a+b)^2=a^2+2ab+b^2 \\ \\ (a-b)^2=a^2-2ab+b^2 \end{gathered}`

Now let's complete it!

`\begin{gathered} x^2+4x=y^2-4y-4\text{ complete adding 4 on both sides} \\ \\ x^2+4x+4=y^2-4y-4+4 \\ \\ (x+2)^2=y^2-4y \\ \end{gathered}`

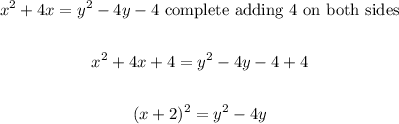
We already completed one side, now let's complete the side with y^2, see that we will add 4 again, then

`\begin{gathered} (x+2)^2=y^2-4y \\ \\ (x+2)^2+4=y^2-4y+4 \\ \\ (x+2)^2+4=(y-2)^2 \end{gathered}`

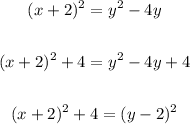
And now we can write it using the standard equation!

`\begin{gathered} (y-2)^2-(x+2)^2=4 \\ \\ (y-2)^2-(x+2)^2=4 \\ \\ ((y-2)^2)/(4)-((x+2)^2)/(4)=1 \end{gathered}`

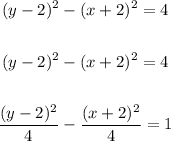
And now we can graph it like all other hyperbolas, the vertices will be:

`(-2,4)\text{ and }(-2,0)`

And the foci

`\begin{gathered} c^2=a^2+b^2 \\ \\ c^2=2^2+2^2 \\ \\ c^2=2\cdot2^2 \\ \\ c^{}=2\, \sqrt[]{2} \end{gathered}`

Then the foci are

`(-2,2+2\, \sqrt[]{2})\text{ and }(-2,2-2\, \sqrt[]{2})`

Now we can plot the hyperbola!