Question

Can u find a b and c its parallelogramthank u

Answer 1

To answer this question, we need to remember two theorems of parallelograms:

1. If a quadrilateral is a parallelogram, the two sets of its opposite angles are congruent:

2. The consecutive angles of parallelograms are supplementary (they sum 180 degrees):

Then, with this information, we have that:

`97\cong m\angle c\Rightarrow m\angle c=97`

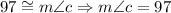
And also, we have that the diagonal forms two congruent triangles, and the sum of internal angles of a triangle is equal to 180, then, we have:

`m\angle c+26+m\angle b=180\Rightarrow97+26+m\angle b=180\Rightarrow m\angle b=180-97-26`

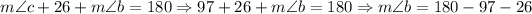
Then, we have:

`m\angle b=180-123\Rightarrow m\angle b=57`

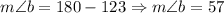
Then, using that the consecutive angles of parallelograms are supplementary (they sum 180 degrees), we have:

`97+m\angle a+m\angle b=180\Rightarrow97+m\angle a+57=180\Rightarrow m\angle a=180-97-57_{}`

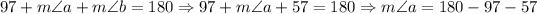
Thus, we have that the measure for angle a is:

`m\angle a=180-154\Rightarrow m\angle a=26`

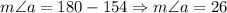
In summary, we have that (all the measures in degrees):

m< a = 26

m< b = 57

m< c = 97