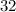Let N be the total amount of whole ounces that are mailed.
Since mailing the first ounce has a cost of $0.39, then there will be N-1 ounces charged for $0.22 each.
The total cost of mailing N ounces will be:
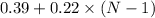
If that cost cannot exceed $7.24, then:
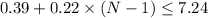
Solve the inequality for N:

Since N must be a whole number, the maximum value of N that satisfies the inequality is 32.
Therefore, the maximum number of whole ounces that can be mailed for $7.24 is: