Question

Which expression is equivalent to cot2B(1 – cos-B) for all values of ß for which cot2B(1 - cos2B) is defined?

Answer 1

From the Pythagorean identity,

`\sin ^2\beta+\cos ^2\beta=1`

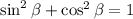
we have

`\sin ^2\beta=1-\cos ^2\beta`

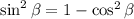
Then, the given expression can be rewritten as

`\cot ^2\beta\sin ^2\beta\ldots(a)`

On the other hand, we know that

`\begin{gathered} \cot \beta=(\cos\beta)/(\sin\beta) \\ \text{then} \\ \cot ^2\beta=(\cos^2\beta)/(\sin^2\beta) \end{gathered}`

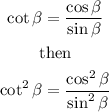
Then, by substituting this result into equation (a), we get

`\begin{gathered} (\cos^2\beta)/(\sin^2\beta)\sin ^2\beta \\ (\cos ^2\beta*\sin ^2\beta)/(\sin ^2\beta) \end{gathered}`

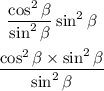
so by canceling out the squared sine, we get

`\cos ^2\beta`

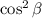
Therefore, the answer is the last option