Question

Sort the sequences according to whether they are arithmetic, geometric, or neither. (98.3, 94.1, 89.9, 85.7,) (1, 0, -1, 0) (1.75, 3.5, 7, 14) (-12, -10.8, -9.6, -8.4) (-1, 1, -1, 1)

Answer 1

hello

to know what type of sequence they are, we need to test either for common difference of common ratio

first sequence

(98.3, 94.1, 89.9)

first term = 98.3

in this case there's a common difference here

we can find that by subtracting the second term from the first term or the third term from the second term

`\text{common difference (d) = 94.1-98.3=-4.2}`

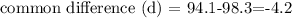
first sequence is an arithmetic progression

second sequence

(1, 0, -1, 0)

first term = 1

common difference or common ratio does not exist here

third sequence

(1.75, 3.5, 7, 14)

first term = 1.75

in this case, there's no common difference but rather common ratio

common ratio (r) can be found by dividing the second term by the first term or the third term by the second term

`\begin{gathered} \text{common ratio(r) = }(3.5)/(1.75)=2 \\ (14)/(7)=2 \end{gathered}`

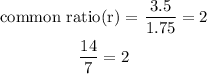
the common ratio here is 2 and this is a geometric progression

fourth sequence

(-12, -10.8, -9.8, -8.4)

first term = -12

in this sequence, there's no common difference or common ratio

fifth sequence

(-1, 1, -1, 1)

the fifth sequence is neither a geometric or artimethic progression because there no common difference or ratio