Question

which of the following additional statements would you need to prove these two triangles are by SAS similarity?

Answer 1

∠I ≅∠L

Explanation:

Answer 2

∠I ≅∠L

1) Given that the triangles are similar, then we can write:

`\begin{gathered} (KL)/(HI)=(JL)/(GI) \\ (18)/(12)=(27)/(18)\text{ =}(3)/(2) \end{gathered}`

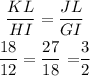
Notice that the sides are proportional to k=3/2.

2) Since we need to prove that these triangles are similar under SAS -Side, Angle Side, examining the picture we can state that one of their corresponding angles are congruent so

`\begin{gathered} \angle I\cong\angle L \\ \end{gathered}`

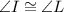
3) Having one of these angles as congruent would fit to prove that these triangles are similar by SAS similarity.