The area A of a circle is given by
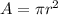
where Pi is 3.1416 and r is the radius. In our case, we get
![100\operatorname{mm}=\pi r^2]()
and we need to find r. In this regard, if we move Pi to the left hand side we get
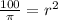
then, r is given by
![r=\sqrt[]{(100)/(\pi)}](https://img.qammunity.org/2023/formulas/mathematics/college/fo53dxjd5tas3ig0t7jvv3r1u0ffwq1y9s.png)
Now, the circunference C is given by
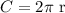
then, by substituting our last result into this formula, we have
![C=2\pi\sqrt[]{(100)/(\pi)}](https://img.qammunity.org/2023/formulas/mathematics/college/vwielimn9rfstvyynhrxjbm6graninumsu.png)
since square root of 100 is 10, we get
![C=2\pi\frac{10}{\sqrt[]{\pi}}](https://img.qammunity.org/2023/formulas/mathematics/college/4qvzsruv6yflh1seh3i68s50vcl3pwqmeg.png)
we can rewrite this result as
![\begin{gathered} C=\frac{2\pi*10}{\sqrt[]{\pi}} \\ C=\frac{2\sqrt[]{\pi\text{ }}\sqrt[]{\pi}*10}{\sqrt[]{\pi}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4ki0bmyk7jezn13nlask6cibqybp5d9ymw.png)
and we can cancel out a square root of Pi. Then, we have
![C=2\sqrt[]{\pi}*10](https://img.qammunity.org/2023/formulas/mathematics/college/h4lr6wvr6ul459yjgz8axtd8dbu6cfxbsq.png)
and the circunference is
![C=20\text{ }\sqrt[]{\pi}\text{ milimeters}](https://img.qammunity.org/2023/formulas/mathematics/college/kj0kyg8pfgw0wbt2uqzbjuj45y5yow201n.png)