Answer:
(-3, 2)
Explanation:
Given the system of inequalities:
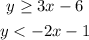
To solve the inequalities graphically, follow the steps below:
Inequality 1
First, find the equation of the boundary line.
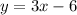
Next, determine the intercepts to draw the boundary line.
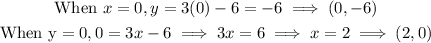
Join the points (0,-6) and (2,0) using a solid line.
Finally, determine the required half-plane using the origin test.
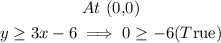
The side that contains the point (0,0) is the required half-plane.
The graph showing the first inequality is given below:
Inequality 2
First, find the equation of the boundary line.
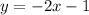
Next, determine the intercepts to draw the boundary line.
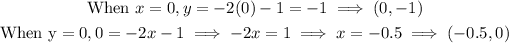
Join the points (0,-1) and (-0.5,0) using a broken line.
Finally, determine the required half-plane using the origin test.

The side that DOES NOT contain the point (0,0) is the required half-plane.
The graph of the system of inequalities is given below:
A point in the solution set is (-3, 2).