Question

The mean amount of time it takes a kidney stone to pass is 16 days and the standard deviation is 5 days. Suppose that one individual is randomly chosen. Let X = time to pass the kidney stone. Round all answers to 4 decimal places where possible.a. What is the distribution of X? X ~ N(16Correct,5Correct) b. Find the probability that a randomly selected person with a kidney stone will take longer than 17 days to pass it. 0.2Incorrectc. Find the minimum number for the upper quarter of the time to pass a kidney stone. 0.8Incorrect days.

Answer 1

• (a)X ~ N(16, 5)

,

• (b)0.4207

,

• (c)19.37 days

Explanation:

(a)

• The mean amount of time = 16 days

,

• The standard deviation = 5 days.

Therefore, the distribution of X is:

`X\sim N(16,5)`

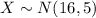
(b)P(X>17)

To find the required probabability, recall the z-score formula:

`z=(X-\mu)/(\sigma)`

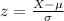
When X=17

`z=(17-16)/(5)=(1)/(5)=0.2`

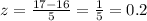
Next, find the probability, P(x>0.2) from the z-score table:

`P(x>0.2)=0.4207`

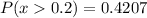
The probability that a randomly selected person with a kidney stone will take longer than 17 days to pass it is 0.4207.

(c)The upper quarter is the value under which 75% of data points are found.

The z-score associated with the 75th percentile = 0.674.

We want to find the value of X when z=0.674.

`\begin{gathered} z=(X-\mu)/(\sigma) \\ 0.674=(X-16)/(5) \\ \text{ Cross multiply} \\ X-16=5*0.674 \\ X=16+(5*0.674) \\ X=19.37 \end{gathered}`

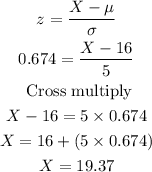
The minimum number for the upper quarter of the time to pass a kidney stone is 19.37 days.