Question

Find angle a in the taper shown,x = 9.342 inchesy = 6.692 inchesz = 2.952 inches

Answer 1

We need to find angle a in the figure.

We know that:

x = 9.342 inches

y = 6.692 inches

z = 2.952 inches

We can do so by finding the legs in the following triangle:

The adjacent leg is x. And the opposite leg is found by subtracting z from y, and then dividing the result by two (assuming the figure is symmetric):

`(y-z)/(2)`

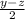
Thus, we have:

`\begin{gathered} \sin a=\frac{\text{ opposite leg}}{\text{ adjacent leg}} \\ \\ \sin a=((y-z)/(2))/(x) \\ \\ \sin a=((6.692-2.952)/(2))/(9.342) \\ \\ \sin a=(1.87)/(9.342) \\ \\ a=\arcsin\left((1.87)/(9.342)\right) \\ \\ a\cong11.55\degree \end{gathered}`