Question

Solve this system of linear equations. Separatethe x- and y-values with a comma.18x - 10y = 749x - 9y = 45

Answer 1

Given,

`\begin{gathered} \text{The system of pair of linear equation is,} \\ 18x-10y=74\ldots\ldots\ldots\ldots\ldots.\ldots.(i) \\ 9x-9y=45\ldots\ldots\ldots..\ldots\ldots\ldots.(ii) \end{gathered}`

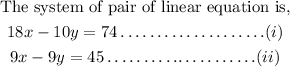
Multiplying equation (ii) by 2 as it make the coefficent of x in both equation equal.

`\begin{gathered} 18x-10y=74\ldots\ldots\ldots\ldots\ldots.\ldots.(i) \\ 18x-18y=90\ldots\ldots\ldots..\ldots\ldots\ldots.(iii) \\ \end{gathered}`

Substracting equation (i) from equation (iii) then we get,

`\begin{gathered} 18x-18y-(18x-10y)=90-74 \\ 18x-18y-18x+10y=16 \\ -8y=16 \\ y=-2 \end{gathered}`

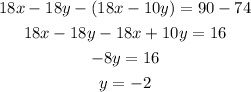
The value of y is -2.

Substituting the value of y in equation (i) then,

`\begin{gathered} 18x-10y=74 \\ 18x+20=74 \\ 18x=54 \\ x=3 \end{gathered}`

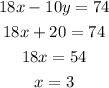
Hence, the solution of the linear pair (x, y) is (3, -2).