To find the coefficients we first need to make the multipliation on the left expression:
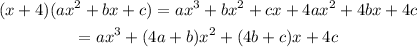
Then we have:
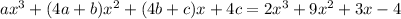
Two polynomials are equal if and only if their coefficients are equal, this leads to the following equations:
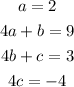
From the first one it is clear that the value of a is 2, from the last one we have:
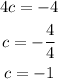
Plugging the value of a in the second one we have:
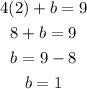
Therefore, we conclude that a=2, b=1 and c=-1 and the correct choice is D.