As observed from the graph, the curve is a straight line from point (-2,-1) to (-5,2).
Consider that the equation of a straight line passing through two points is given by,
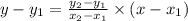
So the equation of the line passing through (-2,-1) and (-5,2) is given by,
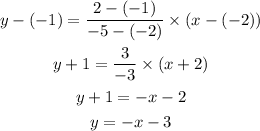
Note that this function is only for the interval [-2, -5].
Now, the value of 'y' corresponding to the input x=-4 is calculated as,

Thus, the required output is y = 1 .