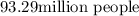The formula for the logistic regression model that best fits the data is,
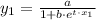
The graph, tables and details of the population data will be shown below
a) The equation that best fits the regression model is,
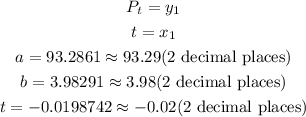
Substitutes the data above into the equation
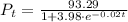
Hence,
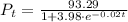
b) In the year 2030, t = 20
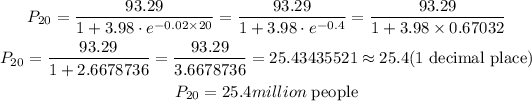
Hence, the answer is

c) Given that
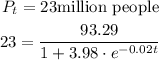
Multiply both sides by 1+3.98e^{-0.02t}
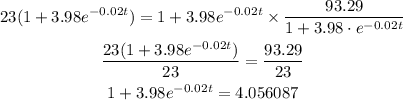
Subtract 1 from both sides

Divide both sides by 3.98
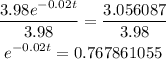
Apply exponent rule

Divide both sides by -0.02
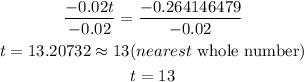
Hence, the population will reach 23million in the year 2023.
d) The carrying capacity for Florida's population is equal to the value of a.
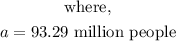
Hence, the carrying capacity fof Florida's population is