The product of the slopes of the perpendicular lines is -1, which means if the slope of one of them is m, then the slope of the perpendicular line is -1/m
In triangle ABC
The perpendicular bisector of the side BC is drawn from the opposite vertex A
Then to find it find the slope of BC and reciprocal it and change its sign to get its slope and find the midpoint of BC to use it in the equation of the perpendicular bisector
Since B = (7, 3) and C = (4, 6)
Let us find the slope of BC, using the rule of the slope
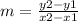
Let (x1, y1) = (7, 3) and (x2, y2) = (4, 6)
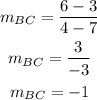
Now to find the slope of the perpendicular line to BC reciprocal it and change its sign
Since the reciprocal of 1 is 1 and the opposite of negative is positive, then
Then the slope of the perpendicular line is 1
Now, let us find the mid-point of BC
The rule of the midpoint is
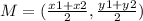
Then the mid-point of BC is
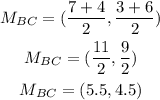
Now we can form the equation of the perpendicular bisector of BC using its slope 1 and the point (5.5, 4.5)
The form of the equation using a point and a slope is
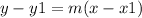
m is the slope and (x1, y1) is a point on the line
Since m = 1 and (x1, y1) = (5.5, 4.5), then
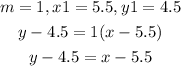
Add 4.5 to both sides
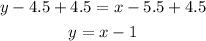
The equation of the perpendicular bisector of BC is
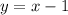
We will do the same to AB and AC