Question

Solve the inequalities|4x + 5| +  2  >  10

Answer 1

We have to solve this inequality:

`\begin{gathered} |4x+5|+2>10 \\ |4x+5|>10-2 \\ |4x+5|>8 \end{gathered}`

We now use the properties of the absolute value. We will have two boundaries: one corresponding to when 4x+5 is negative and the other is when 4x+5 is positive.

When 4x+5 is negative, the absolute value function will change the sign of the expression, so we will have:

`\begin{gathered} -(4x+5)>8 \\ -4x-5>8 \\ -4x>8+5 \\ -4x>13 \\ x<(13)/(-4) \\ x<-3.25 \end{gathered}`

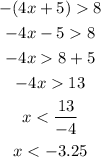
The other interval will be defined when 4x+5 is positive. In this case, the absolute function does not change the sign and we get:

`\begin{gathered} 4x+5>8 \\ 4x>8-5 \\ 4x>3 \\ x>(3)/(4) \\ x>0.75 \end{gathered}`

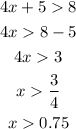
Then, the solution set is the union of the intervals x < -3.25 and x > 0.75.

We can express the interval as (-∞, -3.25) ∪ (0.75, ∞).

Answer: (-∞, -3.25) ∪ (0.75, ∞)