SOLUTION
STEP 1
The hull hypothesis can written as
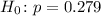
The alternative hypothesis is written as
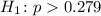
STEP 2
The value of p will be
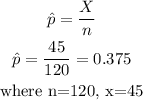
STEP3
From the calculations, we have
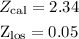
We obtained the p-value has
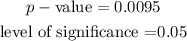
STEP4
Since the p-value is less than the level of significance, we Reject the null hypothesis
STEP 5
Conclusion: There is no enought evidence to support the claim