To find the intersection point between f(x) and g(x) we will equate their right sides
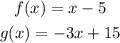
Equate x - 5 by -3x + 15 to find x

add 3x to both sides
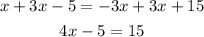
Add 5 to both sides
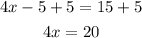
Divide both sides by 4 to get x
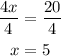
Then the first one is TRUE
For the 2nd one
f(x) = 3, and g(x) = 11 - 2x
If x = 3, then substitute x by 3 in g(x)
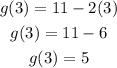
Since f(3) = 3 because it is a constant function and g(x) = 5 at x = 3
That means they do not intersect at x = 3 because f(3), not equal g(3)
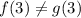
Then the second one is FALSE
For the third one
f(x) = x + 3
at x = 2
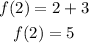
g(x) = -x + 7
at x = 2
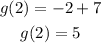
Since f(2) = g(2), then
f(x) intersects g(x) at x = 2
The third one is TRUE
For the fourth one
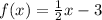
At x = -2
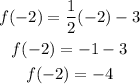
g(x) = -2x + 2
At x = -2
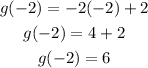
Hence f(-2) do not equal g(-2), then
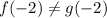
f(x) does not intersect g(x) at x = -2
The fourth one is FALSE