If both triangles are congruent by the HL theorem, then their hypotenuses are equal and at least one of the corresponding legs is equal too.
Hypothenuses:
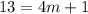
From this expression, you can calculate the value of m
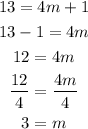
Legs:

Replace the expression with the calculated value of m
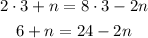
Now pass the n-related term to the left side of the equation and the numbers to the right side:
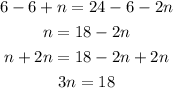
And divide both sides of the expression by 3

So, for m=3 and n=6 the triangles are congruent by HL